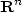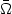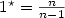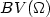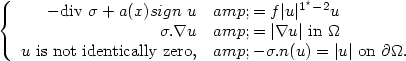Refine listing
Actions for selected content:
Contents
Research Article
Clocks and Insensitivity to Small Measurement Errors
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 537-557
-
- Article
- Export citation
Stability results for some nonlinear elliptic equations involving the p-Laplacian with critical Sobolev growth
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 559-575
-
- Article
- Export citation
Dynamic stabilization of systems via decoupling techniques
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 577-593
-
- Article
- Export citation
Optimal Control of Semilinear Parabolic Equations with State-Constraints of Bottleneck Type
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 595-608
-
- Article
- Export citation
On the Phase Portrait of the Fast Filtering Algorithms
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 609-630
-
- Article
- Export citation
Profil isopérimétrique, métriques périodiques et formes d'équilibre des cristaux
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 631-665
-
- Article
- Export citation
On Some Nonlinear Partial Differential Equations Involving the “1”-Laplacian and Critical Sobolev Exponent
-
- Published online by Cambridge University Press:
- 15 August 2002, pp. 667-686
-
- Article
- Export citation