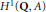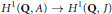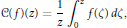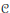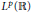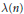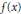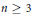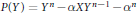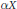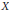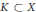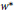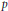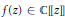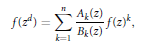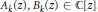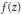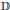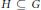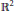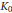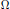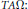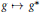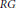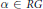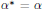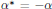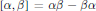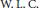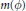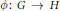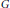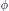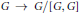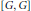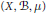Contents
Research Article
On the Notion of Visibility of Torsors
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-228
-
- Article
-
- You have access
- Export citation
Cesàro Operators on the Hardy Spaces of the Half-Plane
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 229-240
-
- Article
-
- You have access
- Export citation
Versions of Schwarz's Lemma for Condenser Capacity and Inner Radius
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 241-250
-
- Article
-
- You have access
- Export citation
Sign Changes of the Liouville Function on Quadratics
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 251-257
-
- Article
-
- You have access
- Export citation
The Smallest Pisot Element in the Field of Formal Power Series Over a Finite Field
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 258-264
-
- Article
-
- You have access
- Export citation
Embedding Distributions of Generalized Fan Graphs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 265-271
-
- Article
-
- You have access
- Export citation
On Super Weakly Compact Convex Sets and Representation of the Dual of the Normed Semigroup They Generate
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 272-282
-
- Article
-
- You have access
- Export citation
Transcendental Solutions of a Class of Minimal Functional Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 283-291
-
- Article
-
- You have access
- Export citation
Quasisymmetrically Minimal Moran Sets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 292-305
-
- Article
-
- You have access
- Export citation
Real Hypersurfaces in Complex Projective Space Whose Structure Jacobi Operator is Lie 𝔻-parallel
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 306-316
-
- Article
-
- You have access
- Export citation
A Note on Conjectures of F. Galvin and R. Rado
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 317-325
-
- Article
-
- You have access
- Export citation
Restricting Fourier Transforms of Measures to Curves in ℝ2
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 326-336
-
- Article
-
- You have access
- Export citation
Certain Properties of K0-monoids Preserved by Tracial Approximation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 337-343
-
- Article
-
- You have access
- Export citation
Involutions and Anticommutativity in Group Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 344-353
-
- Article
-
- You have access
- Export citation
The Sizes of Rearrangements of Cantor Sets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 354-365
-
- Article
-
- You have access
- Export citation
Multiple Solutions for Nonlinear Periodic Problems
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 366-377
-
- Article
-
- You have access
- Export citation
Sharp Threshold of the Gross-Pitaevskii Equation with Trapped Dipolar Quantum Gases
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 378-387
-
- Article
-
- You have access
- Export citation
Application of Measure of Noncompactness to Infinite Systems of Differential Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 388-394
-
- Article
-
- You have access
- Export citation
Coessential Abelianization Morphisms in the Category of Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 395-399
-
- Article
-
- You have access
- Export citation
A Factorization Theorem for Multiplier Algebras of Reproducing Kernel Hilbert Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 400-406
-
- Article
-
- You have access
- Export citation