Let f be a $C^2$ diffeomorphism on a compact manifold. Ledrappier and Young introduced entropies along unstable foliations for an ergodic measure $\mu $ . We relate those entropies to covering numbers in order to give a new upper bound on the metric entropy of $\mu $ in terms of Lyapunov exponents and topological entropy or volume growth of sub-manifolds. We also discuss extensions to the $C^{1+\alpha },\,\alpha>0$ , case.

We give a lower estimate for the central value μ*n(e) of the nth convolution power μ*···*μ of a symmetric probability measure μ on a polycyclic group G of exponential growth whose support is finite and generates G. We also give a similar large time diagonal estimate for the fundamendal solution of the equation (∂/∂t + L)u = 0, where L is a left invariant sub-Laplacian on a unimodular amenable Lie group G of exponential growth.

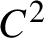
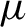
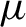
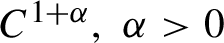
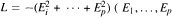We prove a homogenization formula for a sub-Laplacian are left invariant Hörmander vector fields) on a connected Lie group 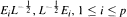Gof polynomial growth. Then using a rescaling argument inspired from M. Avellanedaand F. H. Lin [2], we prove Harnack inequalities for the positive solutions of the equation (∂/∂t+ L)u= 0. Using these inequalities and further exploiting the algebraic structure of Gwe prove that the Riesz transforms , are bounded on Lq,1 < q <+∞ and from L1to weak-L1.