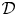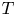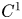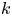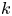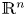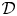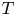Refine search
Actions for selected content:
2 results
Involutivity of distributions at points of superdense tangency with respect to normal currents
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 24 March 2023, pp. 508-524
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The identity G(D)f = F for a linear partial differential operator G(D). Lusin type and structure results in the non-integrable case
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 26 November 2020, pp. 1893-1919
- Print publication:
- December 2021
-
- Article
- Export citation