We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this note, we will prove that a finite-dimensional Lie algebra L over a field of characteristic zero, admitting an abelian algebra of derivations D≤Der(L), with the property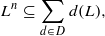 
for some n>1, is necessarily solvable. As a result, we show that if L has a derivation d:L→L such that Ln⊆d(L), for some n>1, then L is solvable.
