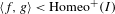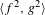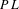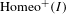Refine search
Actions for selected content:
1 results
2-chains and square roots of Thompson’s group
 $F$
$F$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 25 March 2019, pp. 2515-2532
- Print publication:
- September 2020
-
- Article
- Export citation