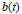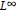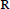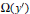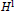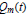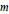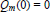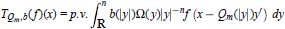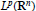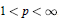Refine search
Actions for selected content:
9 results
On a Singular Integral of Christ–Journé Type with Homogeneous Kernel
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 1 / 01 March 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 97-113
- Print publication:
- 01 March 2018
-
- Article
-
- You have access
- Export citation
A NOTE ON MARCINKIEWICZ INTEGRALS ASSOCIATED TO SURFACES OF REVOLUTION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 14 August 2017, pp. 380-402
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
Some Estimates for Generalized Commutators of Rough Fractional Maximal and Integral Operators on Generalized Weighted Morrey Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 1 / 01 March 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 131-145
- Print publication:
- 01 March 2017
-
- Article
-
- You have access
- Export citation
On the Generalized Marcinkiewicz Integral Operators with Rough Kernels
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 1 / 01 March 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 100-112
- Print publication:
- 01 March 2011
-
- Article
-
- You have access
- Export citation
The Parabolic Littlewood–Paley Operator with Hardy Space Kernels
-
- Journal:
- Canadian Mathematical Bulletin / Volume 52 / Issue 4 / 01 December 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 521-534
- Print publication:
- 01 December 2009
-
- Article
-
- You have access
- Export citation
A PARABOLIC SINGULAR INTEGRAL OPERATOR WITH ROUGH KERNEL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 163-179
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
$L^{p}$ BOUNDS FOR MARCINKIEWICZ INTEGRALS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 46 / Issue 3 / October 2003
- Published online by Cambridge University Press:
- 10 December 2003, pp. 669-677
-
- Article
-
- You have access
- Export citation
A problem on rough parametric Marcinkiewicz functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 13-22
- Print publication:
- February 2002
-
- Article
-
- You have access
- Export citation
Lp -Boundedness of a Singular Integral Operator
-
- Journal:
- Canadian Mathematical Bulletin / Volume 41 / Issue 4 / 01 December 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 404-412
- Print publication:
- 01 December 1998
-
- Article
-
- You have access
- Export citation
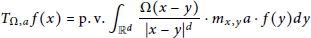
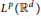
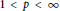
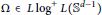
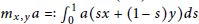
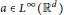
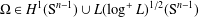

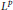




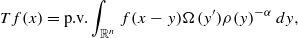
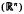
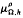 with kernel function Ω in
with kernel function Ω in 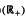 +) for 1 < q ≦.
+) for 1 < q ≦.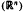
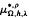 and
and 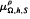 with Ω in
with Ω in 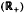
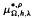 and
and 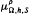 are parametric Marcinkiewicz functions corresponding to the Littlewood-Paley
are parametric Marcinkiewicz functions corresponding to the Littlewood-Paley