Refine search
Actions for selected content:
1 results
A Fourier Companion Matrix (Multiplication Matrix) with Real-Valued Elements: Finding the Roots of a Trigonometric Polynomial by Matrix Eigensolving
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 6 / Issue 4 / November 2013
- Published online by Cambridge University Press:
- 28 May 2015, pp. 586-599
- Print publication:
- November 2013
-
- Article
- Export citation
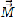 is a multiplication matrix in the sense that, after first defining a vector
is a multiplication matrix in the sense that, after first defining a vector 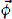 whose elements are the first 2
whose elements are the first 2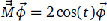 . This relationship is the eigenproblem; the zeros
. This relationship is the eigenproblem; the zeros 