We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
If μk,n(α,β) denotes the relative extrema of the Jacobi polynomial P(α,β)n(x), ordered so that μk+1,n(α,β) lies to the left of μk,n(α,β), then R. A. Askey has conjectured twenty years ago that for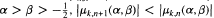 
for k = 1,…, n — 1 and n = 1,2,=. In this paper, we give an asymptotic expansion for μk,n(α,β) when k is fixed and n → ∞, which corrects an earlier result of R. Cooper (1950). Furthermore, we show that Askey's conjecture is true at least in the asymptotic sense.
