Pierre Barrucand asks the following question (Unsolved Problems, # ASI 88:04, Banff, May 1988, Richard K. Guy, Ed.; also [2, p. 594]). Let K be a cyclic quartic field, and let ξ be a non-square element of K. Let M be the Galois closure of 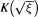 , and let G be the Galois group Gal(M/Q). Find (1) all possible G, (2) conditions on ξ to have such a G, and (3) a list of all possible subfields of M.
, and let G be the Galois group Gal(M/Q). Find (1) all possible G, (2) conditions on ξ to have such a G, and (3) a list of all possible subfields of M.