We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We give continuous separation theorems for convex sets in a real linear space equipped with a norm that can assume the value infinity. In such a space, it may be impossible to continuously strongly separate a point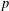 
$p$ from a closed convex set not containing 
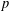$p$, that is, closed convex sets need not be weakly closed. As a special case, separation in finite-dimensional extended normed spaces is considered at the outset.
