In this work, we consider the periodic boundary value problem 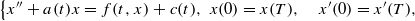 where a,c∈L1(0,T) and f is a Carathéodory function. An existence theorem for positive periodic solutions is proved in the case where the associated Green function is nonnegative. Our result is valid for systems with strong singularities, and answers partially the open problem raised in Torres [‘Weak singularities may help periodic solutions to exist’, J. Differential Equations232 (2007), 277–284].
where a,c∈L1(0,T) and f is a Carathéodory function. An existence theorem for positive periodic solutions is proved in the case where the associated Green function is nonnegative. Our result is valid for systems with strong singularities, and answers partially the open problem raised in Torres [‘Weak singularities may help periodic solutions to exist’, J. Differential Equations232 (2007), 277–284].