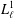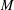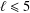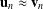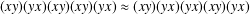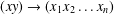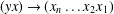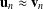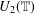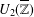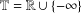Refine search
Actions for selected content:
2 results
LEE MONOIDS ARE NONFINITELY BASED WHILE THE SETS OF THEIR ISOTERMS ARE FINITELY BASED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 422-434
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
THE FINITE BASIS PROBLEM FOR THE MONOID OF TWO-BY-TWO UPPER TRIANGULAR TROPICAL MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 08 January 2016, pp. 54-64
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation