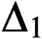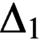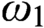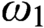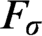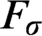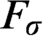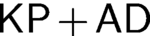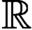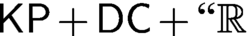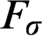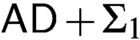Refine search
Actions for selected content:
3 results
PROVABLY
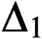 $\Delta_1$ GAMES
$\Delta_1$ GAMES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 30 October 2020, pp. 1124-1146
- Print publication:
- September 2020
-
- Article
- Export citation
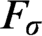 $F_\sigma $ GAMES AND REFLECTION IN
$F_\sigma $ GAMES AND REFLECTION IN 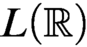 $L(\mathbb {R})$
$L(\mathbb {R})$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 21 July 2020, pp. 1102-1123
- Print publication:
- September 2020
-
- Article
- Export citation
PERFECT SUBSETS OF GENERALIZED BAIRE SPACES AND LONG GAMES
-
- Journal:
- The Journal of Symbolic Logic / Volume 82 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 09 January 2018, pp. 1317-1355
- Print publication:
- December 2017
-
- Article
- Export citation