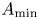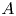Refine search
Actions for selected content:
2 results
General kernel estimates of Schrödinger-type operators with unbounded diffusion terms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 19 May 2023, pp. 929-960
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Extreme values and kernel estimates of point processes boundaries
-
- Journal:
- ESAIM: Probability and Statistics / Volume 8 / August 2004
- Published online by Cambridge University Press:
- 15 September 2004, pp. 150-168
- Print publication:
- August 2004
-
- Article
- Export citation