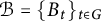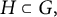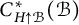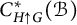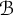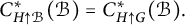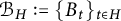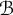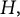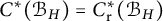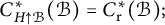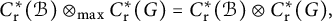Refine search
Actions for selected content:
89 results
2 - Falsification, Paradigms and Research Programmes
-
- Book:
- Explanation and Critical Thinking in the Neurosciences
- Published online:
- 17 December 2025
- Print publication:
- 22 January 2026, pp 22-43
-
- Chapter
- Export citation
3 - Logical Fallacies
-
- Book:
- Explanation and Critical Thinking in the Neurosciences
- Published online:
- 17 December 2025
- Print publication:
- 22 January 2026, pp 44-96
-
- Chapter
- Export citation
Chapter 4 - “All the Logic I think Proper to Employ”
-
-
- Book:
- Hume's <i>A Treatise of Human Nature</i>
- Published online:
- 05 December 2025
- Print publication:
- 08 January 2026, pp 64-78
-
- Chapter
- Export citation
Chapter 6 - A New Natural Theology
- from Part III - A Program for a Positive Jewish Theology
-
- Book:
- Reviving Jewish Theology
- Published online:
- 20 November 2025
- Print publication:
- 04 December 2025, pp 143-170
-
- Chapter
- Export citation
40 - Leveraging Action Research to Create Innovative P-12 Systems Change in School–University Partnerships
- from Part VI - Inquiry and Innovation in School–University Partnerships
-
-
- Book:
- The Cambridge Handbook of School–University Partnerships
- Published online:
- 05 November 2025
- Print publication:
- 07 August 2025, pp 637-658
-
- Chapter
- Export citation
Chapter 2.2 - Intravenous Anaesthetic Agents
- from Sec 2 - Pharmacology
-
- Book:
- Dr Podcast Scripts for the Primary FRCA
- Published online:
- 19 June 2025
- Print publication:
- 03 July 2025, pp 184-196
-
- Chapter
- Export citation
4 - Electrodynamics
-
- Book:
- Electromagnetism
- Published online:
- 26 June 2025
- Print publication:
- 19 June 2025, pp 107-141
-
- Chapter
- Export citation
Case 29 - A 40-Year-Old Presents at 34 Weeks’ Gestation with Absent Fetal Movement
- from Section 3 - Antepartum (Late Pregnancy)
-
-
- Book:
- Pregnancy Complications
- Published online:
- 08 April 2025
- Print publication:
- 01 May 2025, pp 89-91
-
- Chapter
- Export citation

An Introduction to the Philosophy of Science
-
- Published online:
- 29 March 2025
- Print publication:
- 27 March 2025
-
- Textbook
- Export citation
1 - Some Problems of Induction
- from Part I - Background and Basic Concepts
-
- Book:
- An Introduction to the Philosophy of Science
- Published online:
- 29 March 2025
- Print publication:
- 27 March 2025, pp 3-14
-
- Chapter
- Export citation
2 - Algebras and Coalgebras
-
- Book:
- Initial Algebras and Terminal Coalgebras
- Published online:
- 30 January 2025
- Print publication:
- 06 February 2025, pp 12-64
-
- Chapter
- Export citation
1 - Introduction
-
- Book:
- Initial Algebras and Terminal Coalgebras
- Published online:
- 30 January 2025
- Print publication:
- 06 February 2025, pp 1-11
-
- Chapter
- Export citation

Probability and Inductive Logic
-
- Published online:
- 30 January 2025
- Print publication:
- 30 January 2025
-
- Element
- Export citation
Cross-sectional C*-algebras associated with subgroups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 19 December 2024, pp. 1-26
-
- Article
- Export citation
8 - An ExpressiveTheory of Expressions
-
- Book:
- The Road to Paradox
- Published online:
- 17 October 2024
- Print publication:
- 31 October 2024, pp 143-204
-
- Chapter
- Export citation
Chapter 6 - Generative Intelligence
- from Part II - Transition Expertise
-
- Book:
- Transition Expertise and Identity
- Published online:
- 30 May 2024
- Print publication:
- 06 June 2024, pp 92-109
-
- Chapter
- Export citation
Chapter 8 - Aristotle on the Stages of Cognitive Development
-
-
- Book:
- Conceptualising Concepts in Greek Philosophy
- Published online:
- 25 April 2024
- Print publication:
- 02 May 2024, pp 178-202
-
- Chapter
-
- You have access
- Open access
- HTML
- Export citation
Chapter 4 - Creating Questions
-
- Book:
- Pragmatism and Methodology
- Published online:
- 04 January 2024
- Print publication:
- 25 January 2024, pp 74-96
-
- Chapter
-
- You have access
- Open access
- HTML
- Export citation
5 - The WTO Agreement as a Law of Rights
-
- Book:
- A Communitarian Theory of WTO Law
- Published online:
- 14 December 2023
- Print publication:
- 21 December 2023, pp 256-325
-
- Chapter
- Export citation
Natural Kinds: The Expendables
-
- Journal:
- Canadian Journal of Philosophy / Volume 53 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 10 November 2023, pp. 103-120
-
- Article
-
- You have access
- Open access
- HTML
- Export citation