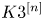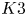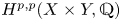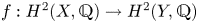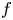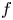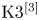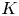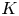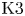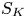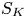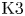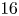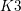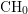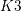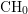Refine search
Actions for selected content:
4 results
MUKAI’S PROGRAM FOR NONPRIMITIVE CURVES ON K3 SURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 17 March 2025, pp. 1053-1091
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rational Hodge isometries of hyper-Kähler varieties of
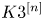 $K3^{[n]}$ type are algebraic
$K3^{[n]}$ type are algebraic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 07 May 2024, pp. 1261-1303
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sixfolds of generalized Kummer type and K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 388-410
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Derived categories of
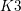 $K3$ surfaces, O’Grady’s filtration, and zero-cycles on holomorphic symplectic varieties
$K3$ surfaces, O’Grady’s filtration, and zero-cycles on holomorphic symplectic varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 26 November 2019, pp. 179-197
- Print publication:
- January 2020
-
- Article
- Export citation