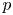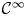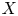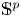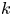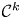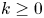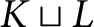Refine search
Actions for selected content:
17 results

Polygraphs: From Rewriting to Higher Categories
-
- Published online:
- 18 March 2025
- Print publication:
- 03 April 2025
Approximation and homotopy in regulous geometry
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 09 November 2023, pp. 1-20
- Print publication:
- January 2024
-
- Article
- Export citation
4 - Differentiable Manifolds
-
- Book:
- Mathematical Methods for Physics
- Published online:
- 08 December 2022
- Print publication:
- 22 December 2022, pp 99-169
-
- Chapter
- Export citation
On the homotopy and strong homotopy type of complexes of discrete Morse functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 February 2022, pp. 19-37
- Print publication:
- March 2023
-
- Article
- Export citation
The genesis of the groupoid model
-
- Journal:
- Mathematical Structures in Computer Science / Volume 31 / Issue 9 / October 2021
- Published online by Cambridge University Press:
- 29 December 2020, pp. 1003-1005
-
- Article
- Export citation
Shortest paths in arbitrary plane domains
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 09 November 2020, pp. 349-367
- Print publication:
- April 2022
-
- Article
- Export citation
7 - Left Bousfield Localisation
-
- Book:
- Foundations of Stable Homotopy Theory
- Published online:
- 09 March 2020
- Print publication:
- 26 March 2020, pp 317-375
-
- Chapter
- Export citation

Foundations of Stable Homotopy Theory
-
- Published online:
- 09 March 2020
- Print publication:
- 26 March 2020
28 - The ’t Hooft–Polyakov Monopole Solution and Topology
- from Part II - Solitons and Topology; Non-Abelian Theory
-
- Book:
- Classical Field Theory
- Published online:
- 04 March 2019
- Print publication:
- 14 March 2019, pp 256-266
-
- Chapter
- Export citation
Some results on extension of maps and applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1465-1472
- Print publication:
- December 2019
-
- Article
- Export citation
Interpolation by G2 Quintic Pythagorean-Hodograph Curves
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 7 / Issue 3 / August 2014
- Published online by Cambridge University Press:
- 28 May 2015, pp. 374-398
- Print publication:
- August 2014
-
- Article
- Export citation
A generalization of Ohkawa’s theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 5 / May 2014
- Published online by Cambridge University Press:
- 03 April 2014, pp. 893-902
- Print publication:
- May 2014
-
- Article
- Export citation
DIAGRAMS OF AN ABELIAN GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 1 / August 2009
- Published online by Cambridge University Press:
- 06 July 2009, pp. 38-64
- Print publication:
- August 2009
-
- Article
-
- You have access
- Export citation
Homotopy Formulas for Cyclic Groups Acting on Rings
-
- Journal:
- Canadian Mathematical Bulletin / Volume 51 / Issue 1 / 01 March 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 81-85
- Print publication:
- 01 March 2008
-
- Article
-
- You have access
- Export citation
On the Lack of Inverses to C*-Extensions Related to Property T Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 50 / Issue 2 / 01 June 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 268-283
- Print publication:
- 01 June 2007
-
- Article
-
- You have access
- Export citation
COUNTING HOMOTOPY TYPES OF GAUGE GROUPS
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 81 / Issue 3 / November 2000
- Published online by Cambridge University Press:
- 03 November 2000, pp. 747-768
- Print publication:
- November 2000
-
- Article
- Export citation
Homotopy Theory of Diagrams and CW-Complexes Over a Category
-
- Journal:
- Canadian Journal of Mathematics / Volume 43 / Issue 4 / 01 August 1991
- Published online by Cambridge University Press:
- 20 November 2018, pp. 814-824
- Print publication:
- 01 August 1991
-
- Article
-
- You have access
- Export citation