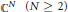Refine search
Actions for selected content:
15 results
A note on the space of all Toeplitz operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 12 November 2024, pp. 1123-1140
- Print publication:
- December 2024
-
- Article
- Export citation
20 - Monomial Convergence in Banach Sequence Spaces
- from Part 3 - Replacing Polydiscs by Other Balls
-
- Book:
- Dirichlet Series and Holomorphic Functions in High Dimensions
- Published online:
- 19 July 2019
- Print publication:
- 08 August 2019, pp 506-530
-
- Chapter
- Export citation
10 - Monomial Convergence of Holomorphic Functions
- from Part 1 - Bohr’s Problem and Complex Analysis on Polydiscs
-
- Book:
- Dirichlet Series and Holomorphic Functions in High Dimensions
- Published online:
- 19 July 2019
- Print publication:
- 08 August 2019, pp 230-267
-
- Chapter
- Export citation
2 - Holomorphic Functions on Polydiscs
- from Part 1 - Bohr’s Problem and Complex Analysis on Polydiscs
-
- Book:
- Dirichlet Series and Holomorphic Functions in High Dimensions
- Published online:
- 19 July 2019
- Print publication:
- 08 August 2019, pp 37-75
-
- Chapter
- Export citation
13 - Hardy Spaces and Holomorphy
- from Part 1 - Bohr’s Problem and Complex Analysis on Polydiscs
-
- Book:
- Dirichlet Series and Holomorphic Functions in High Dimensions
- Published online:
- 19 July 2019
- Print publication:
- 08 August 2019, pp 315-336
-
- Chapter
- Export citation
3 - Bohr’s Vision
- from Part 1 - Bohr’s Problem and Complex Analysis on Polydiscs
-
- Book:
- Dirichlet Series and Holomorphic Functions in High Dimensions
- Published online:
- 19 July 2019
- Print publication:
- 08 August 2019, pp 76-92
-
- Chapter
- Export citation
24 - Vector-Valued Hardy Spaces
- from Part 4 - Vector-Valued Aspects
-
- Book:
- Dirichlet Series and Holomorphic Functions in High Dimensions
- Published online:
- 19 July 2019
- Print publication:
- 08 August 2019, pp 584-611
-
- Chapter
- Export citation

Dirichlet Series and Holomorphic Functions in High Dimensions
-
- Published online:
- 19 July 2019
- Print publication:
- 08 August 2019
Hausdorff operators on holomorphic Hardy spaces and applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1095-1112
- Print publication:
- June 2020
-
- Article
- Export citation
The Spectra of Algebras of Group-Symmetric Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 29 November 2018, pp. 609-623
-
- Article
- Export citation
HOLOMORPHIC FUNCTIONS WITH IMAGE OF GIVEN LOGARITHMIC OR ELLIPTIC CAPACITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 08 March 2013, pp. 145-157
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
ON THE HOLLAND–WALSH CHARACTERIZATION OF BLOCH FUNCTIONS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 51 / Issue 2 / June 2008
- Published online by Cambridge University Press:
- 28 July 2008, pp. 439-441
-
- Article
-
- You have access
- Export citation
Strongly omnipresent operators: general conditions and applications to composition operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 3 / June 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 335-348
- Print publication:
- June 2002
-
- Article
-
- You have access
- Export citation
Holomorphic Functions of Exponential Growth on Abelian Coverings of a Projective Manifold
-
- Journal:
- Compositio Mathematica / Volume 127 / Issue 1 / May 2001
- Published online by Cambridge University Press:
- 04 December 2007, pp. 69-81
- Print publication:
- May 2001
-
- Article
-
- You have access
- Export citation
Each Copy of the Real Line in
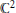 is Removable
is Removable
-
- Journal:
- Canadian Mathematical Bulletin / Volume 44 / Issue 1 / 01 March 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 126-128
- Print publication:
- 01 March 2001
-
- Article
-
- You have access
- Export citation
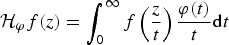
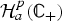
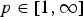
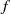
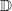
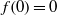
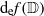
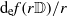
 is Removable
is Removable