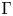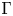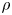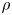Refine search
Actions for selected content:
6 results
Non-local approximation of free-discontinuity problems in linear elasticity and application to stochastic homogenisation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 08 June 2023, pp. 1060-1094
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Brittle fracture in linearly elastic plates
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 19 November 2021, pp. 68-103
- Print publication:
- February 2023
-
- Article
- Export citation
Quasistatic crack evolution for a cohesive zone modelwith different response to loading and unloading:a Young measures approach
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 17 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 09 October 2009, pp. 1-27
- Print publication:
- January 2011
-
- Article
- Export citation
A relaxation result for energies defined on pairs set-function and applications
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 13 / Issue 4 / October 2007
- Published online by Cambridge University Press:
- 20 July 2007, pp. 717-734
- Print publication:
- October 2007
-
- Article
- Export citation
Discrete approximation of the Mumford-Shah functionalin dimension two
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 33 / Issue 4 / July 1999
- Published online by Cambridge University Press:
- 15 August 2002, pp. 651-672
- Print publication:
- July 1999
-
- Article
- Export citation
Finite-differences discretizations of the mumford-shah functional
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 33 / Issue 2 / March 1999
- Published online by Cambridge University Press:
- 15 August 2002, pp. 261-288
- Print publication:
- March 1999
-
- Article
- Export citation