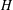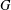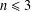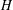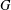Refine search
Actions for selected content:
2 results
TRANSVERSALS AS GENERATING SETS IN FINITELY GENERATED GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 19 August 2015, pp. 47-60
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
CLOSED SUBGROUPS OF PROFINITE GROUPS
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 81 / Issue 1 / July 2000
- Published online by Cambridge University Press:
- 01 July 2000, pp. 29-54
- Print publication:
- July 2000
-
- Article
- Export citation