Refine search
Actions for selected content:
3 results
Determining sets for holomorphic functions on the symmetrized bidisk
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 31 January 2023, pp. 984-996
- Print publication:
- September 2023
-
- Article
- Export citation
Borderline gradient continuity for fractional heat type operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 14 October 2022, pp. 1651-1682
- Print publication:
- October 2023
-
- Article
- Export citation
Extension and averaging operators for finite fields
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 30 April 2013, pp. 599-614
-
- Article
-
- You have access
- Export citation
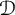
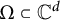
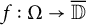
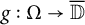
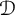

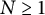
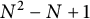
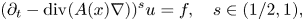
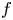
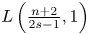
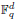 :
: 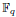 with
with 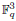 , due to Mockenhaupt and Tao, to the
, due to Mockenhaupt and Tao, to the 