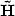Refine search
Actions for selected content:
14 results
7 - Modelling Internal and External Geomagnetic Fields Using Satellite Data
- from Part II - Geomagnetic Field
-
-
- Book:
- Geomagnetism, Aeronomy and Space Weather
- Published online:
- 25 October 2019
- Print publication:
- 14 November 2019, pp 84-97
-
- Chapter
- Export citation
Part II - Geomagnetic Field
-
- Book:
- Geomagnetism, Aeronomy and Space Weather
- Published online:
- 25 October 2019
- Print publication:
- 14 November 2019, pp 39-112
-
- Chapter
- Export citation
Mesh Quality and More Detailed Error Estimates of Finite Element Method
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 09 May 2017, pp. 420-436
- Print publication:
- May 2017
-
- Article
- Export citation
Modification and Numerical Method for the Jiles-Atherton Hysteresis Model
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 07 February 2017, pp. 763-781
- Print publication:
- March 2017
-
- Article
- Export citation
A New Two-Grid Method for Expanded Mixed Finite Element Solution of Nonlinear Reaction Diffusion Equations
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 17 January 2017, pp. 757-774
- Print publication:
- June 2017
-
- Article
- Export citation
A Discrete-Ordinate Discontinuous-Streamline Diffusion Method for the Radiative Transfer Equation
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 5 / November 2016
- Published online by Cambridge University Press:
- 02 November 2016, pp. 1443-1465
- Print publication:
- November 2016
-
- Article
- Export citation
Estimating tree biomass and changes in root biomass following clear-cutting of Brachystegia-Julbernardia (miombo) woodland in central Zambia
-
- Journal:
- Environmental Conservation / Volume 41 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 18 June 2013, pp. 54-63
-
- Article
- Export citation
A posteriori error estimation for semilinearparabolic optimal control problems with application to model reduction by POD∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 47 / Issue 2 / March 2013
- Published online by Cambridge University Press:
- 21 January 2013, pp. 555-581
- Print publication:
- March 2013
-
- Article
- Export citation
Error Estimation for Neglecting Unsteady Hydrodynamic Forces in the Equation of Motion for an Immersed Pendulum
-
- Journal:
- Journal of Mechanics / Volume 29 / Issue 1 / March 2013
- Published online by Cambridge University Press:
- 20 December 2012, pp. 1-6
- Print publication:
- March 2013
-
- Article
- Export citation
Reliability of germination testing of ex situ conserved seeds: a genebank case study on outsourced analyses
-
- Journal:
- Plant Genetic Resources / Volume 10 / Issue 2 / August 2012
- Published online by Cambridge University Press:
- 11 May 2012, pp. 134-136
-
- Article
- Export citation
An Analytical Method for the Inverse Cauchy Problem of Laplace Equation in a Rectangular Plate
-
- Journal:
- Journal of Mechanics / Volume 27 / Issue 4 / December 2011
- Published online by Cambridge University Press:
- 07 December 2011, pp. 575-584
- Print publication:
- December 2011
-
- Article
- Export citation
SICODYN international benchmark on dynamic analysis ofstructure assemblies: variability and numerical-experimental correlation on an industrialpump
-
- Journal:
- Mechanics & Industry / Volume 11 / Issue 6 / November 2010
- Published online by Cambridge University Press:
- 22 December 2010, pp. 439-451
- Print publication:
- November 2010
-
- Article
- Export citation
A new H(div)-conforming p-interpolation operatorin two dimensions
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 45 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 02 August 2010, pp. 255-275
- Print publication:
- March 2011
-
- Article
- Export citation
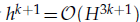 . An numerical example is also given to illustrate the effectiveness of the algorithm.
. An numerical example is also given to illustrate the effectiveness of the algorithm.