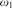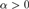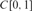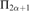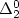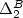Refine search
Actions for selected content:
6 results
 $\Delta ^1_1$ EFFECTIVIZATION IN BOREL COMBINATORICS
$\Delta ^1_1$ EFFECTIVIZATION IN BOREL COMBINATORICS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 17 May 2024, pp. 943-967
- Print publication:
- September 2025
-
- Article
- Export citation
RANDOMNESS VIA INFINITE COMPUTATION AND EFFECTIVE DESCRIPTIVE SET THEORY
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 766-789
- Print publication:
- June 2018
-
- Article
- Export citation
JUMP OPERATIONS FOR BOREL GRAPHS
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 01 May 2018, pp. 13-28
- Print publication:
- March 2018
-
- Article
- Export citation
A LIGHTFACE ANALYSIS OF THE DIFFERENTIABILITY RANK
-
- Journal:
- The Journal of Symbolic Logic / Volume 79 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 17 April 2014, pp. 240-265
- Print publication:
- March 2014
-
- Article
- Export citation
Weihrauch degrees, omniscience principles and weak computability
-
- Journal:
- The Journal of Symbolic Logic / Volume 76 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 12 March 2014, pp. 143-176
- Print publication:
- March 2011
-
- Article
- Export citation
Hierarchies of function classes defined by the first-value operator
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 42 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 25 December 2007, pp. 253-270
- Print publication:
- April 2008
-
- Article
- Export citation