We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
A probability measure-preserving action of a discrete amenable group G is said to be dominant if it is isomorphic to a generic extension of itself. Recently, it was shown that for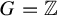 
$G = \mathbb {Z}$, an action is dominant if and only if it has positive entropy and that for any G, positive entropy implies dominance. In this paper, we show that the converse also holds for any G, that is, that zero entropy implies non-dominance.
An ergodic dynamical system 
$\mathbf {X}$ is called dominant if it is isomorphic to a generic extension of itself. It was shown by Glasner et al [On some generic classes of ergodic measure preserving transformations. Trans. Moscow Math. Soc. 82(1) (2021), 15–36] that Bernoulli systems with finite entropy are dominant. In this work, we show first that every ergodic system with positive entropy is dominant, and then that if 
$\mathbf {X}$ has zero entropy, then it is not dominant.
