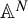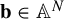Refine search
Actions for selected content:
2 results
Minimally critical regular endomorphisms of
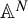 $\mathbb{A}^N$
$\mathbb{A}^N$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 21 October 2021, pp. 585-614
- Print publication:
- February 2023
-
- Article
- Export citation
Degree gaps for multipliers and the dynamical André–Oort conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 13 November 2020, pp. 867-876
- Print publication:
- December 2021
-
- Article
- Export citation