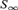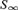Refine search
Actions for selected content:
3 results
COMPUTABLE POLISH GROUP ACTIONS
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 01 August 2018, pp. 443-460
- Print publication:
- June 2018
-
- Article
- Export citation
LEFT-ORDERABLE COMPUTABLE GROUPS
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 05 February 2018, pp. 237-255
- Print publication:
- March 2018
-
- Article
- Export citation
On Computable Field Embeddings and Difference Closed Fields
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 6 / 01 December 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1338-1363
- Print publication:
- 01 December 2017
-
- Article
-
- You have access
- Export citation