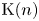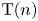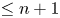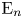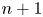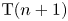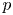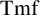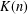Refine search
Actions for selected content:
4 results
Higher semiadditive algebraic K-theory and redshift
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 15 December 2023, pp. 237-287
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ELLIPTIC COHOMOLOGY IS UNIQUE UP TO HOMOTOPY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 15 November 2022, pp. 99-118
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
6 - Monoidal Structures
-
- Book:
- Foundations of Stable Homotopy Theory
- Published online:
- 09 March 2020
- Print publication:
- 26 March 2020, pp 234-316
-
- Chapter
- Export citation
MORAVA MODULES AND THE
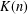 $K(n)$-LOCAL PICARD GROUP
$K(n)$-LOCAL PICARD GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 06 July 2015, pp. 171-172
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation