Refine search
Actions for selected content:
7 results
Relative vertex asphericity
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 16 June 2020, pp. 292-305
- Print publication:
- June 2021
-
- Article
- Export citation
A new test for asphericity and diagrammatic reducibility of group presentations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 871-895
- Print publication:
- April 2020
-
- Article
- Export citation
On the Asphericity of a Family of Positive Relative Group Presentations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 05 January 2017, pp. 545-564
-
- Article
- Export citation
ASPHERICAL LABELLED ORIENTED TREES AND KNOTS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 44 / Issue 2 / June 2001
- Published online by Cambridge University Press:
- 20 January 2009, pp. 285-294
-
- Article
-
- You have access
- Export citation
ON THE ASPHERICITY OF LENGTH-6 RELATIVE PRESENTATIONS WITH TORSION-FREE COEFFICIENTS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 51 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 04 February 2008, pp. 201-214
-
- Article
-
- You have access
- Export citation
On the Asphericity of Knot Complements
-
- Journal:
- Canadian Journal of Mathematics / Volume 45 / Issue 2 / 01 April 1993
- Published online by Cambridge University Press:
- 20 November 2018, pp. 340-356
- Print publication:
- 01 April 1993
-
- Article
-
- You have access
- Export citation
Elementary amenable groups and 4-manifolds with Euler characteristic 0
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 1 / February 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 160-170
- Print publication:
- February 1991
-
- Article
-
- You have access
- Export citation
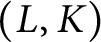
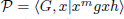 for
for 