Search

Let X be a regular noetherian scheme of finite Krull dimension with involution σ and 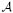an Azumaya algebra over X with involution τ of the second kind with respect to σ. We construct a hermitian and a skew-hermitian Gersten-Witt complex for (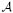, τ) and show that these complexes are exact if X = Spec R is the spectrum of a regular semilocal ring R of geometric type, such that R is a quadratic étale extension of the fixed ring of σ.

Let $X$ be a noetherian scheme with dualizing complex and ${\mathcal{A}}$ a coherent ${\mathcal O}_{X}$-algebra with involution of the first kind $\tau$. We develop in this work a coherent hermitian Witt theory for $({\mathcal{A}},\tau)$. As an application we construct a Gersten–Witt spectral sequence which converges to the coherent hermitian Witt theory of $({\mathcal{A}},\tau)$. We show then that the associated Gersten–Witt complex is exact if $X$ is the spectrum of a smooth semilocal ring and ${\mathcal{A}}$ is locally free as ${\mathcal O}_{X}$-module.

Search Results

Refine search

Refine search

Actions for selected content:

2 results

A Gersten-Witt complex for hermitian Witt groups of coherent algebras over schemes II: Involution of the second kind

A Gersten–Witt complex for hermitian Witt groups of coherent algebras over schemes, I: Involution of the first kind

Search Results

Refine search

Refine search

Actions for selected content:

Save Search

2 results

A Gersten-Witt complex for hermitian Witt groups of coherent algebras over schemes II: Involution of the second kind

A Gersten–Witt complex for hermitian Witt groups of coherent algebras over schemes, I: Involution of the first kind