Floating objects will drift due to the action of surface gravity waves. This drift will depart from that of a perfect Lagrangian tracer due to both viscous effects (non-potential flow) and wave–body interaction (potential flow). We examine the drift of freely floating objects in regular (non-breaking) deep-water wave fields for object sizes that are large enough to cause significant diffraction. Systematic numerical simulations are performed using a hybrid numerical solver, qaleFOAM, which deals with both viscosity and wave–body interaction. For very small objects, the model predicts a wave-induced drift equal to the Stokes drift. For larger objects, the drift is generally greater and increases with object size (we examine object sizes up to 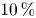 $10\,\%$ of the wavelength). The effects of different shapes, sizes and submergence depths and steepnesses are examined. Furthermore, we derive a ‘diffraction-modified Stokes drift’ akin to Stokes (Trans. Camb. Phil. Soc., vol. 8, 1847, pp. 411–455), but based on the combination of incident, diffracted and radiated wave fields, which are based on potential-flow theory and obtained using the boundary element method. This diffraction-modified Stokes drift explains both qualitatively and quantitatively the increase in drift. Generally, round objects do not diffract the wave field significantly and do not experience a significant drift enhancement as a result. For box-shape objects, drift enhancement is greater for larger objects with greater submergence depths (we report an increase of
$10\,\%$ of the wavelength). The effects of different shapes, sizes and submergence depths and steepnesses are examined. Furthermore, we derive a ‘diffraction-modified Stokes drift’ akin to Stokes (Trans. Camb. Phil. Soc., vol. 8, 1847, pp. 411–455), but based on the combination of incident, diffracted and radiated wave fields, which are based on potential-flow theory and obtained using the boundary element method. This diffraction-modified Stokes drift explains both qualitatively and quantitatively the increase in drift. Generally, round objects do not diffract the wave field significantly and do not experience a significant drift enhancement as a result. For box-shape objects, drift enhancement is greater for larger objects with greater submergence depths (we report an increase of 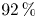 $92\,\%$ for simulations without viscosity and
$92\,\%$ for simulations without viscosity and 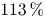 $113\,\%$ with viscosity for a round-cornered box whose size is
$113\,\%$ with viscosity for a round-cornered box whose size is 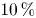 $10\,\%$ of the wavelength). We identify the specific standing wave pattern that arises near the object because of diffraction as the main cause of the enhanced drift. Viscosity plays a small positive role in the enhanced drift behaviour of large objects, increasing the drift further by approximately
$10\,\%$ of the wavelength). We identify the specific standing wave pattern that arises near the object because of diffraction as the main cause of the enhanced drift. Viscosity plays a small positive role in the enhanced drift behaviour of large objects, increasing the drift further by approximately 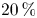 $20\,\%$.
$20\,\%$.