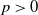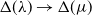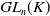Refine search
Actions for selected content:
3 results
On homomorphisms into Weyl modules corresponding to partitions with two parts
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 11 July 2022, pp. 272-283
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hoeffding spaces and Specht modules
-
- Journal:
- ESAIM: Probability and Statistics / Volume 15 / 2011
- Published online by Cambridge University Press:
- 15 October 2010, pp. S58-S68
- Print publication:
- 2011
-
- Article
- Export citation
Representations of Ariki–Koike algebras and Gröbner–Shirshov bases
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 89 / Issue 1 / July 2004
- Published online by Cambridge University Press:
- 30 June 2004, pp. 54-70
- Print publication:
- July 2004
-
- Article
- Export citation