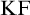 $\mathrm {KF}$
,
$\mathrm {KF}$
,
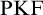 $\mathrm {PKF}$
, AND REINHARDT’S PROGRAM
$\mathrm {PKF}$
, AND REINHARDT’S PROGRAM