Refine search
Actions for selected content:
5 results
Stability of linear stochastic difference equations in strategically controlled random environments
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 4 / December 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 961-981
- Print publication:
- December 2003
-
- Article
- Export citation
Asymptotics of locally-interacting Markov chains with global signals
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 2 / June 2002
- Published online by Cambridge University Press:
- 01 July 2016, pp. 416-440
- Print publication:
- June 2002
-
- Article
- Export citation
A central limit theorem for random coefficient autoregressive models and ARCH/GARCH models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 1 / March 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 113-121
- Print publication:
- March 1998
-
- Article
- Export citation
Generalized adaptive exponential smoothing procedures
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 673-690
- Print publication:
- September 1994
-
- Article
- Export citation
Asymptotic properties of a certain class of Bush–Mosteller learning models
-
- Journal:
- Advances in Applied Probability / Volume 12 / Issue 4 / December 1980
- Published online by Cambridge University Press:
- 01 July 2016, pp. 922-941
- Print publication:
- December 1980
-
- Article
- Export citation
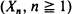 is modified into some adaptive variants and also generalized to the recursive scheme
is modified into some adaptive variants and also generalized to the recursive scheme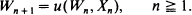 . A broad class of ‘smoothing functions'
. A broad class of ‘smoothing functions' 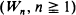 with nice statistical properties, is presented. A method to estimate the limit of the expected smoothed values is also developed.,
with nice statistical properties, is presented. A method to estimate the limit of the expected smoothed values is also developed.,