Refine search
Actions for selected content:
2 results
The Group of Automorphisms of the Algebra of one-Sided Inverses of a Polynomial Algebra. II
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 3 / October 2015
- Published online by Cambridge University Press:
- 03 June 2015, pp. 543-580
-
- Article
-
- You have access
- Export citation
A NOTE ON 2-LOCAL MAPS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 49 / Issue 3 / October 2006
- Published online by Cambridge University Press:
- 25 January 2007, pp. 701-708
-
- Article
-
- You have access
- Export citation
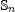 of one-sided inverses of a polynomial algebra
of one-sided inverses of a polynomial algebra 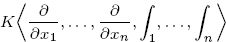
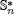 of units of
of units of