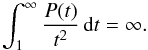We study the regularity of finite energy solutions to degeneraten-harmonic equations. The functionK(x), which measures the degeneracy, is assumed to besubexponentially integrable, i.e. it verifies the condition exp(P(K)) ∈ Lloc1. The function P(t) is increasing on [0,∞[ and satisfies the divergence condition \begin{equation}\int_1^\infty\frac{P(t)}{t^2}\,{\rm d}t=\infty.\end{equation}