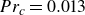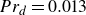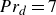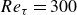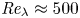Refine search
Actions for selected content:
142 results
Tab orientation effect on jet mixing
-
- Journal:
- The Aeronautical Journal , First View
- Published online by Cambridge University Press:
- 14 November 2025, pp. 1-23
-
- Article
-
- You have access
- HTML
- Export citation
Heat transfer in drop-laden low-Prandtl-number channel turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 1015 / 25 July 2025
- Published online by Cambridge University Press:
- 16 July 2025, A19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Taylor dispersion of bubble swarms rising in quiescent liquid
-
- Journal:
- Journal of Fluid Mechanics / Volume 1014 / 10 July 2025
- Published online by Cambridge University Press:
- 26 June 2025, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dispersive mixing: within or between pores?
-
- Journal:
- Journal of Fluid Mechanics / Volume 1006 / 10 March 2025
- Published online by Cambridge University Press:
- 12 March 2025, F1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
19 - Inertial confinement fusion implosion
- from Part 3 - From the Microscopic to Cosmic Scales
-
- Book:
- Hydrodynamic Instabilities and Turbulence
- Published online:
- 27 June 2024
- Print publication:
- 19 December 2024, pp 385-406
-
- Chapter
- Export citation
1 - Overview of Turbulent Flows
-
- Book:
- Fundamentals of Turbulent Flows
- Published online:
- 09 January 2025
- Print publication:
- 12 December 2024, pp 1-38
-
- Chapter
- Export citation
Fast monotonically integrated large eddy simulation solver: validation of a new scalable tool to study and optimize indoor ventilation
-
- Journal:
- Flow: Applications of Fluid Mechanics / Volume 4 / 2024
- Published online by Cambridge University Press:
- 25 October 2024, E23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On transversal Hölder regularity for flat Wieler solenoids
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 10 September 2024, pp. 294-320
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
8 - Oscillations and CP Violation in Quarks
-
- Book:
- Introduction to Elementary Particle Physics
- Published online:
- 08 November 2024
- Print publication:
- 27 June 2024, pp 315-350
-
- Chapter
-
- You have access
- Open access
- HTML
- Export citation
14 - Two languages at a time
- from Part III - Using language
-
- Book:
- First Language Acquisition
- Published online:
- 01 November 2024
- Print publication:
- 20 June 2024, pp 411-436
-
- Chapter
- Export citation
Mixing-Demixing Behavior of Calcium-Ethylammonium Mixtures in Otay Montmorillonite
-
- Journal:
- Clays and Clay Minerals / Volume 31 / Issue 1 / February 1983
- Published online by Cambridge University Press:
- 02 April 2024, pp. 73-74
-
- Article
- Export citation
Topological reconstruction of compact supports of dependent stationary random variables
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 02 April 2024, pp. 1339-1369
- Print publication:
- December 2024
-
- Article
- Export citation
Approximation with ergodic processes and testability
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 23 January 2024, pp. 1040-1059
- Print publication:
- September 2024
-
- Article
- Export citation
4 - Technical Ecstasy
- from Part I - Metal, Technology and Practice
-
-
- Book:
- The Cambridge Companion to Metal Music
- Published online:
- 31 August 2023
- Print publication:
- 14 September 2023, pp 43-56
-
- Chapter
- Export citation
Conditional mixing in deterministic chaos
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 18 August 2023, pp. 1693-1723
- Print publication:
- June 2024
-
- Article
- Export citation
Lagrangian model for passive scalar gradients in turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 964 / 10 June 2023
- Published online by Cambridge University Press:
- 05 June 2023, A39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
5 - Lagrangian and Objective Eulerian Coherent Structures
-
- Book:
- Transport Barriers and Coherent Structures in Flow Data
- Published online:
- 20 February 2023
- Print publication:
- 16 March 2023, pp 141-241
-
- Chapter
- Export citation
Interface models for three-dimensional Rayleigh–Taylor instability
-
- Journal:
- Journal of Fluid Mechanics / Volume 959 / 25 March 2023
- Published online by Cambridge University Press:
- 16 March 2023, A10
-
- Article
- Export citation
1 - Introduction
-
- Book:
- Transport Barriers and Coherent Structures in Flow Data
- Published online:
- 20 February 2023
- Print publication:
- 16 March 2023, pp 1-12
-
- Chapter
-
- You have access
- Export citation
Mixing properties of erasing interval maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 06 March 2023, pp. 408-431
- Print publication:
- February 2024
-
- Article
- Export citation