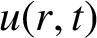Refine search
Actions for selected content:
1 results
A NOTE ON THE AXISYMMETRIC DIFFUSION EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 63 / Issue 3 / July 2021
- Published online by Cambridge University Press:
- 21 July 2021, pp. 333-341
-
- Article
- Export citation