We establish the bounds of Marcinkiewicz integrals associated to surfaces of revolution generated by two polynomial mappings on Triebel–Lizorkin spaces and Besov spaces when their integral kernels are given by functions $\unicode[STIX]{x1D6FA}\in H^{1}(\text{S}^{n-1})\cup L(\log ^{+}L)^{1/2}(\text{S}^{n-1})$. Our main results represent improvements as well as natural extensions of many previously known results.

Under the assumption that $\mu $ is a nondoubling measure, we study certain commutators generated by the Lipschitz function and the Marcinkiewicz integral whose kernel satisfies a Hörmander-type condition. We establish the boundedness of these commutators on the Lebesgue spaces, Lipschitz spaces, and Hardy spaces. Our results are extensions of known theorems in the doubling case.

A class of generalized Marcinkiewicz integral operators is introduced, and, under rather weak conditions on the integral kernels, the boundedness of such operators on ${{L}^{p}}$ and Triebel–Lizorkin spaces is established.

In this paper the authors establish the $L^p$ boundedness for several classes of Marcinkiewicz integral operators with kernels satisfying a condition introduced by Grafakos and Stefanov in Indiana Univ. Math. J.47 (1998), 455–469.

AMS 2000 Mathematics subject classification: Primary 42B25; 42B99

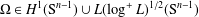
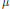
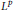
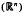
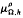In this note the authors give the L2(n) boundedness of a class of parametric Marcinkiewicz integral with kernel function Ω in 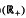L log+L(Sn−1) and radial function h(|x|) ∈ l ∞ l(Lq)(+) for 1 < q ≦.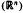

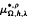As its corollary, the Lp (n)(2 < p < ∞) boundedness of and and 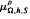with Ω in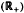 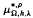L log+L (Sn-1) and h(|x|) ∈ l∞ (Lq)(+) are also obtained. Here and 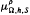are parametric Marcinkiewicz functions corresponding to the Littlewood-Paley g*λ-function and the Lusin area function S, respectively.