Refine search
Actions for selected content:
12 results
Stationary analysis of an (R, Q) inventory model with normal and emergency orders
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 04 October 2022, pp. 106-126
- Print publication:
- March 2023
-
- Article
- Export citation
The moments of the number of exits from a simply connected region
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 1 / March 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 167-180
- Print publication:
- March 1998
-
- Article
- Export citation
Crossings of max-stable processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 130-138
- Print publication:
- March 1994
-
- Article
- Export citation
A note on exceedances and rare events of non-stationary sequences
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 877-888
- Print publication:
- December 1993
-
- Article
- Export citation
Sample path behaviour of Χ 2 surfaces at extrema
-
- Journal:
- Advances in Applied Probability / Volume 20 / Issue 4 / December 1988
- Published online by Cambridge University Press:
- 01 July 2016, pp. 719-738
- Print publication:
- December 1988
-
- Article
- Export citation
An application of the system-point method to inventory models under continuous review
-
- Journal:
- Journal of Applied Probability / Volume 23 / Issue 3 / September 1986
- Published online by Cambridge University Press:
- 14 July 2016, pp. 778-789
- Print publication:
- September 1986
-
- Article
- Export citation
Inventory systems for perishable commodities with renewal input and Poisson output
-
- Journal:
- Advances in Applied Probability / Volume 16 / Issue 2 / June 1984
- Published online by Cambridge University Press:
- 01 July 2016, pp. 402-421
- Print publication:
- June 1984
-
- Article
- Export citation
Level crossings and stationary distributions for general dams
-
- Journal:
- Journal of Applied Probability / Volume 17 / Issue 1 / March 1980
- Published online by Cambridge University Press:
- 14 July 2016, pp. 218-226
- Print publication:
- March 1980
-
- Article
- Export citation
An embedded level crossing technique for dams and queues
-
- Journal:
- Journal of Applied Probability / Volume 16 / Issue 1 / March 1979
- Published online by Cambridge University Press:
- 14 July 2016, pp. 174-186
- Print publication:
- March 1979
-
- Article
- Export citation
Prediction of level crossings for normal processes containing deterministic components
-
- Journal:
- Advances in Applied Probability / Volume 11 / Issue 1 / March 1979
- Published online by Cambridge University Press:
- 01 July 2016, pp. 93-117
- Print publication:
- March 1979
-
- Article
- Export citation
Moments of the exit-time distribution for carboxyhemoglobin due to cigarette smoking
-
- Journal:
- Journal of Applied Probability / Volume 15 / Issue 1 / March 1978
- Published online by Cambridge University Press:
- 14 July 2016, pp. 13-25
- Print publication:
- March 1978
-
- Article
- Export citation
On generalising the notion of upcrossings to random fields
-
- Journal:
- Advances in Applied Probability / Volume 8 / Issue 4 / December 1976
- Published online by Cambridge University Press:
- 01 July 2016, pp. 789-805
- Print publication:
- December 1976
-
- Article
- Export citation
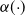

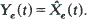 An example of this is the prediction of water level near a coast, when
An example of this is the prediction of water level near a coast, when 