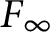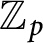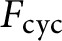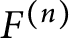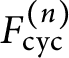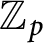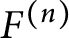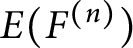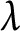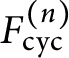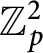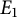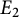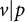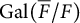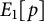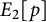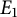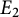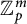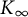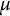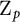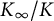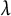Refine search
Actions for selected content:
3 results
Asymptotic growth of Mordell–Weil ranks of elliptic curves in noncommutative towers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 31 January 2022, pp. 1050-1062
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Euler characteristics and their congruences for multisigned Selmer groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 10 January 2022, pp. 298-321
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fine Selmer groups of congruent p-adic Galois representations
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 29 September 2021, pp. 702-722
- Print publication:
- September 2022
-
- Article
- Export citation