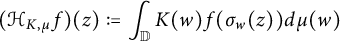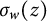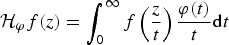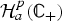Refine search
Actions for selected content:
3 results
Hausdorff operators on some classical spaces of analytic functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 29 February 2024, pp. 768-780
- Print publication:
- September 2024
-
- Article
- Export citation
Hausdorff operators on holomorphic Hardy spaces and applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1095-1112
- Print publication:
- June 2020
-
- Article
- Export citation
Multidimensional Hausdorff operators on the real Hardy space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 1 / August 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 79-86
- Print publication:
- August 2007
-
- Article
-
- You have access
- Export citation