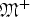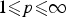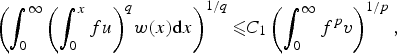Refine search
Actions for selected content:
4 results
Weighted norm inequalities for positive operators restricted on the cone of λ-quasiconcave functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 17-39
- Print publication:
- February 2020
-
- Article
- Export citation
Extremal Sequences for the Bellman Function of the Dyadic Maximal Operator and Applications to the Hardy Operator
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 6 / 01 December 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1364-1384
- Print publication:
- 01 December 2017
-
- Article
-
- You have access
- Export citation
Optimal rearrangement invariant range for Hardy-type operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 12 May 2016, pp. 865-893
- Print publication:
- August 2016
-
- Article
- Export citation
Compactness of Hardy-Type Operators over Star-Shaped Regions in
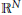 ${{\mathbb{R}}^{N}}$
${{\mathbb{R}}^{N}}$
-
- Journal:
- Canadian Mathematical Bulletin / Volume 47 / Issue 4 / 01 December 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 540-552
- Print publication:
- 01 December 2004
-
- Article
-
- You have access
- Export citation