In this paper, we present explicit and computable error bounds for the asymptotic expansions of the Hermite polynomials with Plancherel–Rotach scale. Three cases, depending on whether the scaled variable lies in the outer or oscillatory interval, or it is the turning point, are considered separately. We introduce the ‘branch cut’ technique to express the error terms as integrals on the contour taken as the one-sided limit of curves approaching the branch cut. This new technique enables us to derive simple error bounds in terms of elementary functions. We also provide recursive procedures for the computation of the coefficients appearing in the asymptotic expansions.

For a general vector field we exhibit two Hilbert spaces, namely the space of so called closed functions and the space of exact functions and we calculate the codimension of the space of exact functions inside the larger space of closed functions. In particular we provide a new approach for the known cases: the Glauber field and the second-order Ginzburg–Landau field and for the case of the fourth-order Ginzburg–Landau field.

We study the asymptotic behavior of the empirical process when theunderlying data are Gaussian and exhibit seasonallong-memory. We prove that the limiting process can be quitedifferent from the limit obtained in the case of regularlong-memory. However, in both cases, the limiting process isdegenerated. We apply our results to von–Mises functionals andU-Statistics.

An Ornstein-Uhlenbeck process subject to a quadratic killing rate is analyzed. The distribution for the process killing time is derived, generalizing the analogous result for Brownian motion. The derivation involves the use of Hermite polynomials in a spectral expansion.

Recently, H. M. Srivastava extended certain interesting generating functions of L. Carlitz to the forms:

and

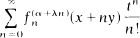
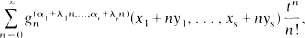
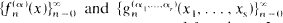where are general oncand many-parameter sequences of functions. In the present paper some general addition formulas for analogous sequences of functions are derived, and a number of interesting applications of the main results are given.

A GI/G/r(x) store is considered with independently and identically distributed inputs occurring in a renewal process, with a general release rate r(·) depending on the content. The (pseudo) extinction time, or the content, just before inputs is a Markov process which can be represented by a random walk on and below a bent line; this results in an integral equation of the form gn+1(y) = ∫ l(y, w)gn(w) dw with l(y, w) a known conditional density function. An approximating solution is found using Hermite or modified Hermite polynomial expansions resulting in a Gram–Charlier or generalized Gram–Charlier representation, with the coefficients being determined by a matrix equation. Evaluation of the elements of the matrix involves two-dimensional numerical integration for which Gauss–Hermite–Laguerre integration is effective. A number of examples illustrate the quality of the approximating procedure against exact and simulated results.