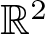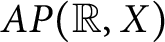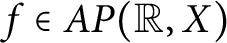Refine search
Actions for selected content:
48 results
Appendix C - Fourier Transforms, Fourier Series, and the FFT Algorithm
-
- Book:
- High-Accuracy Finite Difference Methods
- Published online:
- 16 May 2025
- Print publication:
- 05 June 2025, pp 167-180
-
- Chapter
- Export citation
9 - The Fourier Series
- from Part II - Mathematical Methods
-
- Book:
- An Introduction to Continuum Physics
- Published online:
- 06 February 2025
- Print publication:
- 13 February 2025, pp 489-518
-
- Chapter
- Export citation
4 - Spectral Description of Turbulence
-
- Book:
- Fundamentals of Turbulent Flows
- Published online:
- 09 January 2025
- Print publication:
- 12 December 2024, pp 109-139
-
- Chapter
- Export citation
2 - Review of Mathematics
-
- Book:
- Applied Hydrology
- Published online:
- 09 July 2024
- Print publication:
- 04 July 2024, pp 11-35
-
- Chapter
- Export citation
17 - Mathematical Intricacies*
-
- Book:
- Signals, Systems, and Signal Processing
- Published online:
- 29 August 2024
- Print publication:
- 13 June 2024, pp 638-670
-
- Chapter
- Export citation
6 - Approximation
-
- Book:
- Numerical Methods in Physics with Python
- Published online:
- 30 August 2023
- Print publication:
- 20 July 2023, pp 317-452
-
- Chapter
- Export citation
The Lp convergence of Fourier series on triangular domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 19 June 2023, pp. 453-474
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
6 - Orthonormal Vectors
-
- Book:
- Matrix Mathematics
- Published online:
- 29 September 2023
- Print publication:
- 25 May 2023, pp 111-136
-
- Chapter
- Export citation
4 - The Frequency Domain and Pitch
-
- Book:
- Physics Behind Music
- Published online:
- 24 May 2023
- Print publication:
- 06 April 2023, pp 45-66
-
- Chapter
- Export citation
2 - Linear Invariant Systems and Fourier Analysis
-
- Book:
- Modern Information Optics with MATLAB
- Published online:
- 22 December 2022
- Print publication:
- 05 January 2023, pp 21-69
-
- Chapter
- Export citation
12 - Fourier Series
- from Part II - Constructive Approximation Theory
-
- Book:
- Classical Numerical Analysis
- Published online:
- 29 September 2022
- Print publication:
- 20 October 2022, pp 320-344
-
- Chapter
- Export citation
Appendix E - Fourier Series and Transforms
-
- Book:
- Liquid Crystals and their Computer Simulations
- Published online:
- 21 July 2022
- Print publication:
- 28 July 2022, pp 562-565
-
- Chapter
- Export citation
7 - Fourier Series
- from Part III - Discrete Functional Analysis
-
- Book:
- Classical and Discrete Functional Analysis with Measure Theory
- Published online:
- 06 January 2022
- Print publication:
- 20 January 2022, pp 255-332
-
- Chapter
- Export citation
A note on spaces of almost periodic functions with values in Banach spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 18 January 2022, pp. 953-962
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Classical and Discrete Functional Analysis with Measure Theory
-
- Published online:
- 06 January 2022
- Print publication:
- 20 January 2022
A generalized Davenport expansion
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 26 August 2021, pp. 711-715
-
- Article
- Export citation
11 - Data Analysis: Curve Fitting and Interpolation
- from Part III - Least Squares and Optimization
-
- Book:
- Matrix, Numerical, and Optimization Methods in Science and Engineering
- Published online:
- 18 February 2021
- Print publication:
- 04 March 2021, pp 560-593
-
- Chapter
- Export citation
3 - Diffusion
- from Part I - Basic Thermodynamics and Kinetics of Phase Transformations
-
- Book:
- Phase Transitions in Materials
- Published online:
- 24 April 2020
- Print publication:
- 14 May 2020, pp 59-82
-
- Chapter
- Export citation

Mathematical Methods for Oscillations and Waves
-
- Published online:
- 02 April 2020
- Print publication:
- 05 March 2020
9 - Orthonormal Sets and Orthonormal Bases for Hilbert Spaces
- from Part III - Hilbert Spaces
-
- Book:
- An Introduction to Functional Analysis
- Published online:
- 21 March 2020
- Print publication:
- 12 March 2020, pp 110-125
-
- Chapter
- Export citation