We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We define partial differential (
$\text{PD}$ in the following), i.e., field theoretic analogues of Hamiltonian systems on abstract symplectic manifolds and study their main properties, namely, $\text{PD}$ Hamilton equations, $\text{PD}$ Noether theorem, $\text{PD}$ Poisson bracket, etc. Unlike the standard multisymplectic approach to Hamiltonian field theory, in our formalism, the geometric structure (kinematics) and the dynamical information on the “phase space” appear as just different components of one single geometric object.
A large deviation theorem of the Cramér–Petrov type and a ranking limit theorem of Loève are used to derive an approximation for the statistical distribution of the failure time of fibrous materials. For that, fibrous materials are modeled as a series of independent and identical bundles of parallel filaments and the asymptotic distribution of their failure time is determined in terms of statistical characteristics of the individual filaments, as both the number of filaments in each bundle and the number of bundles in the chain grow large simultaneously. While keeping the number n of filaments in each bundle fixed and increasing only the chain length k leads to a Weibull limiting distribution for the failure time, letting both increase in such a way that log k(n) = o(n), we show that the limit distribution is 
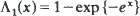for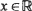 
. Since fibrous materials which are both long and have many filaments prevail, the result is of importance in the materials science area since refined approximations to failure-time distributions can be achieved.
