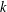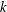Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Login Alert

Cancel

Log in

×

Register

Log In

(0) Cart

Back to search results

Home
Search

Search Results

Refine search

Access:

Only show content I have access to (1)

Content type:

Articles (2)

Author:

Publication date:

Over 3 years (2)

From year:

To year:

Apply From and To filters

Subject: Show more

Mathematics (2)

Actions for selected content:

Select all | Deselect all

View selected items
Save to my bookmarks
Export citations
Download PDF (zip)
Save to Kindle
Save to Dropbox
Save to Google Drive
Save content to
To save content items to your account, please confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your account. Find out more about saving content to .

To save content items to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Please be advised that item(s) you selected are not available.
You are about to save
Your Kindle email address

Please provide your Kindle email.

@free.kindle.com @kindle.com (service fees apply)

By using this service, you agree that you will only keep content for personal use, and will not openly distribute them via Dropbox, Google Drive or other file sharing services

Save Search

You can save your searches here and later view and run them again in "My saved searches".

Search Title: required Please provide a title, maximum of 40 characters.

Cancel

×

2 results

DECIDABILITY AND CLASSIFICATION OF THE THEORY OF INTEGERS WITH PRIMES
ITAY KAPLAN, SAHARON SHELAH
Journal:

The Journal of Symbolic Logic / Volume 82 / Issue 3 / September 2017

Published online by Cambridge University Press:

08 September 2017, pp. 1041-1050

Print publication:

September 2017
- Article
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation
We show that under Dickson’s conjecture about the distribution of primes in the natural numbers, the theory Th (ℤ , +, 1, 0, Pr) where Pr is a predicate for the prime numbers and their negations is decidable, unstable, and supersimple. This is in contrast with Th (ℤ , +, 0, Pr, <) which is known to be undecidable by the works of Jockusch, Bateman, and Woods.

FACTORS OF CARMICHAEL NUMBERS AND A WEAK 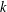$k$-TUPLES CONJECTURE
Part of
- Elementary number theory
THOMAS WRIGHT
Journal:

Journal of the Australian Mathematical Society / Volume 100 / Issue 3 / June 2016

Published online by Cambridge University Press:

17 November 2015, pp. 421-429

Print publication:

June 2016
- Article
- - You have access
- PDF
- Export citation
In light of the recent work by Maynard and Tao on the Dickson $k$-tuples conjecture, we show that with a small improvement in the known bounds for this conjecture, we would be able to prove that for some fixed $R$, there are infinitely many Carmichael numbers with exactly $R$ factors for some fixed $R$. In fact, we show that there are infinitely many such $R$.