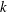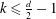Refine search
Actions for selected content:
13 results
14 - Reflections on Coordination in Word-Formation
- from Part III - Syntactic Questions
-
- Book:
- Reflections on English Word-Formation
- Published online:
- 03 October 2025
- Print publication:
- 07 August 2025, pp 110-116
-
- Chapter
- Export citation
6 - Introduction to Calculus
-
- Book:
- Mathematics for Economics and Finance
- Published online:
- 24 May 2024
- Print publication:
- 30 May 2024, pp 51-60
-
- Chapter
- Export citation
9 - Development, Allocation and Management of IP
- from Part II - License Building Blocks
-
- Book:
- Intellectual Property Licensing and Transactions
- Published online:
- 21 June 2022
- Print publication:
- 30 June 2022, pp 248-279
-
- Chapter
-
- You have access
- Open access
- HTML
- Export citation
Derivatives of symplectic eigenvalues and a Lidskii type theorem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 02 December 2020, pp. 457-485
- Print publication:
- April 2022
-
- Article
-
- You have access
- Export citation
17 - Financial markets and financial services
-
- Book:
- Contemporary Australian Corporate Law
- Published online:
- 06 March 2021
- Print publication:
- 28 October 2020, pp 492-562
-
- Chapter
- Export citation
On Homogeneous Polynomials Determined by their Partial Derivatives
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 06 December 2019, pp. 358-365
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
A GAME CHARACTERIZING BAIRE CLASS 1 FUNCTIONS
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 06 June 2019, pp. 456-466
- Print publication:
- March 2020
-
- Article
- Export citation
5 - Calculus
-
- Book:
- The Student's Introduction to <I>Mathematica</I> and the Wolfram Language
- Published online:
- 01 April 2019
- Print publication:
- 16 May 2019, pp 191-248
-
- Chapter
- Export citation
Crop microinsurance: tackling poverty, one insurance policy at a time
-
- Journal:
- Annals of Actuarial Science / Volume 8 / Issue 2 / September 2014
- Published online by Cambridge University Press:
- 15 May 2014, pp. 253-280
-
- Article
- Export citation
FIELDS WITH SEVERAL COMMUTING DERIVATIONS
-
- Journal:
- The Journal of Symbolic Logic / Volume 79 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 17 April 2014, pp. 1-19
- Print publication:
- March 2014
-
- Article
- Export citation
The Galton-Watson process revisited: some martingale relationships and applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 2 / June 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 322-328
- Print publication:
- June 2000
-
- Article
- Export citation
Construction of a Deterministic ω-Automaton Using Derivatives
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 33 / Issue 2 / March 1999
- Published online by Cambridge University Press:
- 15 August 2002, pp. 133-158
- Print publication:
- March 1999
-
- Article
- Export citation
A Continuity-Like Property of Derivatives
-
- Journal:
- Canadian Mathematical Bulletin / Volume 39 / Issue 1 / 01 March 1996
- Published online by Cambridge University Press:
- 20 November 2018, pp. 10-20
- Print publication:
- 01 March 1996
-
- Article
-
- You have access
- Export citation