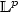We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Considering the centered empirical distribution function F n-F asa variable in ${\mathbb L}^p(\mu)$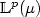 
, we derive non asymptotic upperbounds for the deviation of the ${\mathbb L}^p(\mu)$ 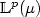-norms ofF n-F as well as central limit theorems for the empirical processindexed by the elements of generalized Sobolev balls. These resultsare valid for a large class of dependent sequences, includingnon-mixing processes and some dynamical systems.
