We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We study the Chern-Ricci flow, an evolution equation of Hermitian metrics, on a family of Oeljeklaus–Toma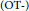 
$\left( \text{OT-} \right)$ manifolds that are non-Kähler compact complex manifolds with negative Kodaira dimension. We prove that after an initial conformal change, the flow converges in the Gromov–Hausdorff sense to a torus with a flat Riemannian metric determined by the 
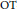$\text{OT}$-manifolds themselves.
